백준 1867 <돌멩이 제거> Python

https://www.acmicpc.net/problem/1867

---

이분매칭 알고리즘을 사용하는 문제입니다.

 

정확하게는 이 문제는 단순한 이분매칭 문제가 아닌 '최소 버텍스 커버(Minimum Vertex Cover)' 문제입니다.

 

최소 버텍스 커버란 무엇인지 먼저 짚고 넘어가겠습니다.

어떠한 그래프가 있습니다.

해당 그래프에서 몇 개의 정점을 고르겠습니다. 과연 몇 개의 정점을 골라야 그래프에 존재하는 모든 간선이 고른 정점과 연결되어 있을까요?

해당 문제의 답을 찾는 것이 바로 최소 버텍스 커버 문제입니다.

 

그렇다면 <돌멩이 제거> 문제는 왜 최소 버텍스 커버 문제일까요?

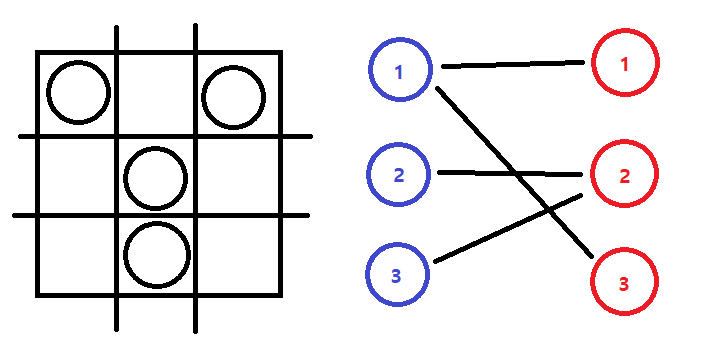
행과 열을 나누어 각각 노드 그룹으로 쪼갠 뒤 돌이 있는 위치의 행 노드와 열 노드를 연결해 그래프를 만든다면 각 간선의 양 끝중 하나의 정점만 선택되어도 해당 간선에 해당되는 돌은 선택되었다고 볼 수 있습니다. 왜냐하면 해당 돌의 위치에 해당하는 행이나 열 둘 중 하나만 선택해 돌을 주으며 지나가도 해당하는 돌을 모두 주울 수 있기 때문입니다. 즉 모든 간선이 선택될 수 있는 최소한의 정점의 수를 구한다면 모든 돌을 선택할 수 있는 최소의 행과 열 개수를 구할 수 있다는 말입니다.

 

예제를 예를 들어 설명하겠습니다.

처음에 2열을 선택했다고 가정하겠습니다.

그렇다면 2열 정점과 연결된 (2-2) 간선과 (3-2) 간선은 선택된 간선이 됩니다. 즉 주운 돌이 되는겁니다.

그리고 1행을 선택하면

모든 간선이 선택되었다 -> 모든 돌을 주웠다가 성립하게 됩니다.

즉 해당 문제는 최소 버텍스 커버 문제로 풀 수 있습니다.

 

그렇다면 최소 버텍스 커버랑 이분매칭이랑은 무슨 상관인데 이 문제가 이분매칭이라는 걸까요?

그건 바로 '쾨니그의 정리' 라는 훌륭한 정리 덕분입니다.

쾨니그의 정리 - 위키백과, 우리 모두의 백과사전

대충 정리하면 이분 그래프에서 최소 버텍스 커버 문제는 이분매칭 문제는 동치, 즉 같은 문제라는 것입니다.

 

덕분에 해당 문제는 이분 그래프에서 최소 버텍스 커버 문제이고, 이분 그래프에서 이분매칭 문제로 풀 수 도 있다는 결론이 나옵니다.

이분 매칭에 대한 자세한 내용은 추후에 다루기로 하겠습니다.

 

그렇다면 이분 매칭은 어떻게 풀어야 할까요?

DFS 를 사용하면 비교적 쉽게 답을 구할 수 있습니다.

 

1. (행/열)노드를 순차적으로 순회하며 연결된 (열/행) 노드를 찾습니다.

2. 연결된 노드가 연결된 다른 노드가 없다면 연결해준 뒤 다음 노드를 순회합니다.

3. 연결된 노드(A)가 이미 다른 노드와 연결되어 있다면(B) B 노드를 다른 노드와 연결시킬 수 있는지 확인합니다.

4. B 노드를 다른 노드와 연결시킬 수 있다면 B 노드를 다른 노드와 연결시킨 뒤 3 에서 순회중이던 노드와 A 노드를 연결한 뒤 다음 노드를 순회합니다.

 

랜덤으로 데이터를 삽입한 예시를 보여드리겠습니다.

해당 모양으로 돌이 놓여져 있다면

 

와 같이 해결 과정을 거치게 됩니다.

---

import sys

input = sys.stdin.readline

# 이분 매칭

def bimatch(idx):

    # 방문했으면 패스

    if visited[idx]:

        return False

    # 방문 체크

    visited[idx] = True

    # 연결될 수 있는 노드 체크

    for node in bi_graph[idx]:

        # 연결되지 않았거나

        # 연결된 노드와 연결된 노드가 다른 노드를 선택할 수 있으면

        if connected[node] < 0 or bimatch(connected[node]):

            # 연결

            connected[node] = idx

            return True    

    return False

def solution(n):

    # 결과

    result = 0

    # 연결 기록(열노드)

    global connected

    connected = [-1 for _ in range(n)]

    # 행노드 순회하며 이분매칭

    for idx in range(n):

        # 방문 기록(행노드)

        global visited

        visited = [False for _ in range(n)]

        if bimatch(idx):

            result += 1

    return result

# 입력

n, k =  map(int, input().strip().split())

bi_graph = [[] for _ in range(n)]

for _ in range(k):

    r, c = map(int, input().strip().split())

    bi_graph[r-1].append(c-1)

print(solution(n))