백준 2252 <줄 세우기> Python

https://www.acmicpc.net/problem/2252

2252번: 줄 세우기

---

위상 정렬 알고리즘을 사용하면 풀 수 있습니다. 간단하게 설명하자면 어떤 노드를 방문하는데 조건이 있는 경우 위상정렬을 사용하게 됩니다.

특정 노드 A 를 방문할 때 B, C 를 선행 방문해야 한다고 가정하겠습니다. A와 B, A 와 C를 간선으로 연결하고, 각 노드에서의 들어오고 나가는 간선을 체크해줍니다.

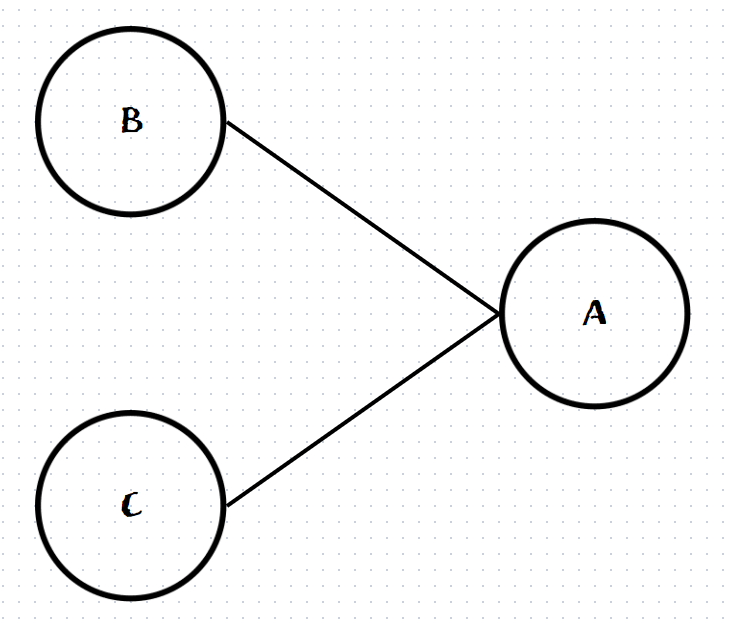
A : 나가는 간선 0 / 들어오는 간선 2

B : 나가는 간선 1 / 들어오는 간선 0

C : 나가는 간선 1 / 들어오는 간선 0

 

우선 들어오는 간선이 0 인 노드를 모두 큐에 집어 넣습니다. 들어오는 간선이 0 이라는 말은 선행 조건이 없다는 말과 같으므로 큐에 넣을 수 있습니다.

queue = [B, C]

 

큐에 넣은 노드와 연결된 노드, 즉 큐에 넣은 노드가 선행 조건인 노드의 들어오는 간선을 -1 해줘야합니다. 해당 노드를 방문하며 선행 조건을 만족했기 때문입니다. 현재 문제에서는 나가는 간선은 신경쓰지 않아도 됩니다.

A : 나가는 간선 0 / 들어오는 간선 2 -1 -1 = 0

B : 나가는 간선 0 / 들어오는 간선 0

C : 나가는 간선 0 / 들어오는 간선 0

 

그리고 BFS 를 사용하는데, 다음 큐에 넣는 조건은 현재 노드와 연결되어 있으면서 들어오는 간선이 0 인 경우입니다. 이를 반복하면 됩니다.

---

import sys

from collections import deque

def solution(N, M, data_list):

    # 큐

    queue = deque([])

    # 위상정렬을 위한 간선정보를 포함한 트리 [[자식 노드들], 들어오는 간선]

    tree = [[[], 0] for _ in range(N+1)]

    tree[0][1] = -1

    # 간선 정보 입력

    for parent, child in data_list:

        # 자식 정보 입력

        tree[parent][0].append(child)

        # 자식의 들어오는 간선 + 1

        tree[child][1] += 1

    # 트리에서 들어오는 간선이 0 인 노드 모두 큐에 추가

    for node_idx in range(len(tree)):

        if not tree[node_idx][1]:

            queue.append(node_idx)

    # 줄세우기 리스트

    line = []

    # 순회

    while True:

        # 큐가 비면 끝

        if not queue:

            print(*line)

            return

        # 현재 노드

        now_node = queue.popleft()

        # 현재 노드 줄세우기 리스트에 추가

        line.append(now_node)

        # 현재 노드의 간선 -1 으로 중복 방지

        tree[now_node][1] -= 1

        # 현재 노드에 연결되어 있는 노드 간선 제거

        for node in tree[now_node][0]:

            tree[node][1] -= 1

        # 현재 노드에 연결되어 있는 노드 중 들어오는 간선이 0 이면 큐에 삽입

        for node in tree[now_node][0]:

            if not tree[node][1]:

                queue.append(node)

N, M = map(int, sys.stdin.readline().split())

data_list = [list(map(int, sys.stdin.readline().split())) for _ in range(M)]

solution(N, M, data_list)